Как найти объем цилиндра: формула и расчеты

Интересуетесь геометрией? Узнайте, как найти объем цилиндра с нашим простым объяснением и формулой. Все, что вам нужно знать о расчете объема цилиндра, представлено в нашей статье «Объем цилиндра». Погрузитесь в мир математики и улучшите свои знания!

{V= \pi R^2 h}

Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон.

Другое определение: цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.

Рассчитать объем цилиндра можно по нескольким формулам. Для расчета необходимо знать высоту цилиндра и один из параметров — радиус основания, диаметр основания или площадь основания.

Содержание:

1. калькулятор объема цилиндра
2. формула объема цилиндра через высоту и радиус
3. формула объема цилиндра через высоту и площадь основания
4. формула объема цилиндра через высоту и диаметр
5. примеры задач

Формула объема цилиндра через высоту и радиус

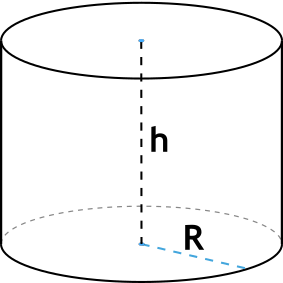
{V= \pi R^2 h}

R — радиус основания цилиндра

h — высота цилиндра

Если внимательно посмотреть на эту формулу, то можно заметить, что {\pi R^2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

Формула объема цилиндра через высоту и площадь основания

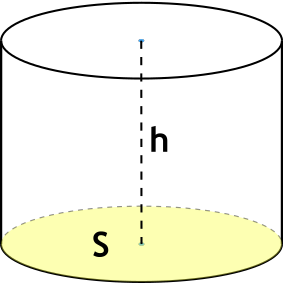
{V= S h}

S — площадь основания цилиндра

h — высота цилиндра

Так как диаметр окружности равен двум радиусам, мы легко можем преобразовать формулу объема цилиндра через радиус и высоту в формулу через диаметр и высоту. Для этого выразим радиус через диаметр и получим необходимую формулу:

D = 2R \to R = \dfrac{D}{2}

V = \pi R^2 h = \pi {\Big( \dfrac{D}{2} \Big) }^2 h = \pi \dfrac{D^2}{4} h

Формула объема цилиндра через высоту и диаметр

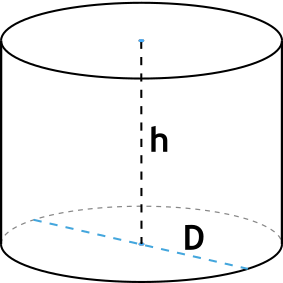
{V= \pi {\dfrac{D^2}{4}} h}

D — диаметр основания цилиндра

h — высота цилиндра

Примеры задач на нахождение объема цилиндра

Задача 1

Найти объём цилиндра с высотой 3см и диаметром основания 6см.

Решение

Так как в условии задачи нам дан диаметр основания цилиндра, мы будем использовать формулу объема через диаметр. Подставим в нее известные высоту и диаметр, чтобы получить объем цилиндра.

V = \pi \dfrac{D^2}{4} h = \pi \dfrac{6^2}{4} 3 = \pi \dfrac{36}{4} 3 = \pi \cdot 9 \cdot 3 = 27 \pi \: см^3 \approx 84.823 \: см^3

Ответ: 27 \pi \: см^3 \approx 84.823 \: см^3

Ответ легко проверить с помощью калькулятора .

Задача 2

Найдите объем цилиндра с радиусом основания 5см и высотой 16см.

Решение

Для решения этой задачи воспользуемся формулой объема через радиус.

V = \pi R^2 h = \pi \cdot 5^2 \cdot 16 = \pi \cdot 25 \cdot 16 = \pi \cdot 25 \cdot 16 = 400 \pi \: см^3 \approx 1 256.63706 \: см^3

Ответ: 400 \pi \: см^3 \approx 1 256.63706 \: см^3

Проверить ответ поможет калькулятор .

Как рассчитать объем формула?

Формула для расчета объема зависит от формы объекта, объем которого необходимо рассчитать. Ниже приведены некоторые примеры расчета объема для различных форм объектов.

1. Объем прямоугольного параллелепипеда:
   Объем = длина x ширина x высота (V = L x W x H)

2. Объем куба:
   Объем = длина ребра x длина ребра x длина ребра (V = a^3)

3. Объем цилиндра:
   Объем = площадь основания x высота (V = πr^2h)

4. Объем конуса:
   Объем = (площадь основания x высота) / 3 (V = (πr^2h) / 3)

5. Объем сферы:
   Объем = (4/3) x π x радиус в кубе (V = (4/3)πr^3)

Здесь L — длина, W — ширина, H — высота, a — длина ребра, r — радиус основания, h — высота.

Обратите внимание, что для расчета объема необходимо измерить соответствующие размеры объекта. Если объект имеет сложную форму, то его объем может быть рассчитан путем разбиения его на более простые фигуры и суммирования их объемов.